Итак, возвращаясь к основному положению: у нас есть восемь основных положений или фаз, в которых могут быть расположены тетраэдр и октаэдр. Однако любой проницательный читатель уже заметил, что восьми основных геометрических положений явно недостаточно для формирования всей Периодической Таблицы; чтобы создать полный набор природных элементов, должны работать еще какие-то дополнительный свойства.

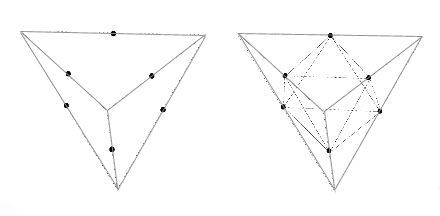
Рис. 4.5 Частотное расширение тетраэдра в октаэдр

Вот ключ:

Обе геометрические формы способны расширяться и сжиматься из своих центров.

Это называется изменением частоты.

Меняя частоту, они формируют разные виды геометрических твердых тел.

Эти твердые тела – не Платоновы, могут быть и другие формы, такие как твердые тела Архимеда, но все они связаны посредством “родительских” тетраэдра и октаэдра.

Как видно на рис. 4.5, сжатие геометрической формы – это деление всех ребер на две или более равных частей, а затем соединение полученных точек. Если мы делим каждое ребро на половины, это называется “второчастотное” деление, если мы делим каждое ребро на три равные части, такое деление называется “третье-частотное” деление. Начиная с тетраэдра, Бакминстер Фуллер продемонстрировал, что посредством процесса расширения или сжатия можно получить всего десять разных частот (геометрических форм), и это центральный аспект находок Джонсона. Например, известно, что “мощная” сила в атомном ядре в десять раз сильнее “слабой” силы в электронных облаках! Обычно это записывается как квадратный корень из 100, равный 10. Никакого иного правдоподобного объяснения этой аномалии не найдено. То есть, ядро представляет собой точку самой “свернутой” геометрии на самом высоком частотном уровне сжатия.

Итак, все, что нужно сделать, - это объединить восемь основных фаз вращающейся в противоположных направлениях геометрии с различными частотами геометрии, возникающей в результате расширения или сжатия. Таким способом можно получить всю Периодическую Таблицу. Кроме того, вы можете предсказать, будет ли элемент твердым, жидкостью или газом, а также, каковы будут его точки замерзания, плавления или испарения. Джонсон направляет заинтересованных мыслителей к работе Джеймса Картера, которому удалось получить всю Периодическую Таблицу посредством схем спиралевидного движения, которые он назвал “круглонами”. И самое интересное: “круглоны” Картера являются сферическими торами! Представляется, что Картер не знал, что спиралевидные, волнообразные, циклические “вращения во вращениях” и были тем, что он изображал между круглонами для демонстрации различных элементов, то есть,  они существуют посредством “абсолютного движения”. В целях более полного описания, мы приглашаем читателя, ознакомиться с нашей детальной статьей и/или вебсайтом Картера. В целях упрощения, мы приведем некоторые наиболее очевидные признаки из квантовой физики, указывающие на работу Платоновых геометрий.