Краеугольным камнем знания секретных школ мистерий, относящегося к скрытому порядку во Вселенной, всегда была сакральная геометрия. Мы достаточно писали на эту тему в двух предыдущих книгах, и для лучшего понимания просим читателя обратиться к этим двум книгам. Сакральная геометрия – это еще одна форма вибрации или “кристализованная” музыка. Рассмотрим следующий пример:

Сначала мы дергаем гитарную струну. Это создает “стоячие волны”, то есть волны, не движущиеся по струне назад и вперед, а остающиеся на одном месте. Мы увидим места, где присутствует сильное вертикальное движение, представляющее собой верх и низ волны, и другие места, где вертикального движения нет. Такие места называются узлами. Узлы, формирующиеся в любом виде стоячей волны, всегда будут расположены на одинаковом расстоянии друг от друга, а скорость вибрации будет определять количество появляющихся узлов. Это значит: чем выше вибрация, тем больше узлов.

В двух измерениях мы можем использовать осциллограф или подвергнуть вибрации плоскую круглую “пластину Хладни” и наблюдать появление узлов, формирующих простые геометрические формы, такие как квадрат, треугольник и шестиугольник. Такая работа повторялась много раз д-ром Гансом Дженни, Джеральдом Хокинсом и другими.

• Если окружность имеет три узла, расположенных на одинаковом расстоянии друг от друга, то при их соединении получится треугольник.

• Если окружность имеет четыре узла, то образуется квадрат.

• Если окружность имеет пять узлов, образуется пятиугольник.

• Шесть узлов образуют шестиугольник, и так далее.

Хотя в терминах волновой механики это очень простая концепция, Джеральд Хокинс первым математически доказал, что вписанные в окружности геометрии являются музыкальными отношениями. Мы, конечно, удивимся, узнав, что к этому открытию его привел анализ различных геометрических образований “кругов на полях”, которые появлялись буквально за одну ночь на полях английской сельской местности. Они описывались в обеих предыдущих книгах.

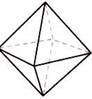
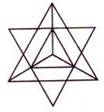
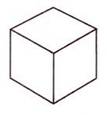
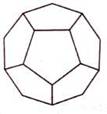
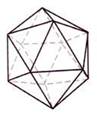
Самые глубинные и самые уважаемые формы священной геометрии трехмерны и известны как Платоновы Твердые Тела. Существуют только пять форм, удовлетворяющих всем необходимым правилам. Это восьмигранный октаэдр, четырехгранный тетраэдр, шестигранный куб, двенадцатигранный додекаэдр и двадцатигранный икосаэдр. На нижеприведенном рисунке тетраэдр изображен в виде “звездного тетраэдра” или сплетенного тетраэдра, что означает два тетраэдра, соединенных вместе в совершенной симметрии.